Calculadora de volume de sólido de revolução
A calculadora de volume de sólido de revolução transforma o cálculo integral em algo palpável. Ou seja basta digitar a função da curva, escolher o eixo (X ou Y), definir o intervalo e selecionar o método disco, arruela ou casca cilíndrica que a ferramenta faz todo o trabalho.
Volume de Sólido de Revolução
Calcule o volume de um sólido gerado pela rotação de uma curva em torno de um eixo usando cálculo integral.
Insira os parâmetros da função na calculadora de volume do sólido de revolução
Como usar a calculadora de volume de sólido de revolução
Função f(x): A função que define a curva a ser rotacionada
Eixo de rotação: Escolha se rotação é em torno do eixo X ou Y
Limite inferior/superior: Intervalo para calcular o volume
Método: Escolha entre disco, arruela ou casca cilíndrica
Clique em Calcular Volume para ver a solução passo a passo.
Sua configuração:
Fórmula e cálculo passo a passo
Fórmula do volume por revolução:
Esta fórmula calcula o volume gerado pela rotação da curva y = f(x) em torno do eixo X.
Insira os parâmetros acima e clique em Calcular Volume.
Assim, você verá o cálculo completo passo a passo!
Volume Calculado!
Exemplos e visualização
Exemplo 1: Parábola (Disco)
Função: f(x) = x²
Eixo: X
Intervalo: [0, 2]
Método: Disco
Volume: ≈ 20.106 unidades³
Exemplo 2: Seno (Arruela)
Função: f(x) = sin(x)
Eixo: X
Intervalo: [0, π]
Método: Arruela (g(x)=0)
Volume: ≈ 4.935 unidades³
Exemplo 3: Raiz Quadrada (Casca)
Função: f(x) = √x
Eixo: Y
Intervalo: [0, 4]
Método: Casca Cilíndrica
Volume: ≈ 33.510 unidades³
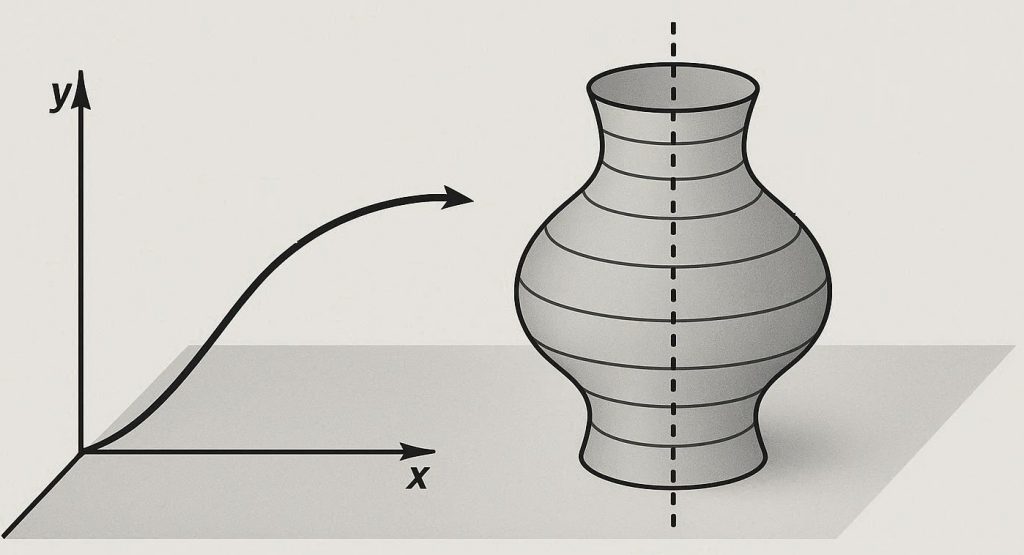
Interpretação Geométrica
Um sólido de revolução é gerado quando uma curva plana gira em torno de um eixo.
Métodos de cálculo:
- Disco: V = π ∫[a,b] [R(x)]² dx
- Arruela: V = π ∫[a,b] ([R(x)]² – [r(x)]²) dx
- Casca: V = 2π ∫[a,b] x·f(x) dx (rotação em Y)
- ∫[a,b]: Integração no intervalo
- V: Volume total do sólido
Aplicações do volume de revolução:
- Engenharia no projeto de tanques e reservatórios
- Arquitetura no design de cúpulas e abóbadas
- Física no cálculo de momentos de inércia
- Design de peças mecânicas rotacionais
- Cálculo de capacidade de recipientes
- Análise de formas orgânicas em biologia
- Projeto de objetos de revolução em CAD
Certamente a calculadora é perfeita para você que está aprendendo cálculo quanto para profissionais que precisam de precisão técnica. Um engenheiro pode estimar a capacidade de um reservatório esférico; um designer, calcular o material necessário para um objeto rotacional; um estudante, conferir seu exercício de ENEM, vestibular ou concursos públicos.