Calculadora de Integração por Frações Parciais
A calculadora de integração por frações parciais é a ferramenta para quem precisa resolver integrais de funções racionais de maneira rápida. Inclusive, esse tipo de cálculo aparece em situações, como no processamento de sinais, na engenharia de controle, na análise de circuitos elétricos e até em modelos econômicos com taxas de crescimento compostas.
Integração por Frações Parciais
Calcule integrais de funções racionais usando o método de frações parciais.
Insira a função racional na calculadora de integração por frações parciais
Como usar a calculadora de frações parciais
Função racional: Digite no formato (ax+b)/(cx+d)
Exemplos: (x+1)/(x^2-1), (2)/(x^2-4)
Grau do numerador: Deve ser menor que o do denominador
Clique em Calcular para ver a decomposição e integral.
Função a decompor:
Decomposição em Frações Parciais
Método das frações parciais:
O método decompõe uma função racional em frações mais simples que são fáceis de integrar.
Insira uma função racional acima e clique em Calcular Frações Parciais.
Você verá a decomposição completa passo a passo!
Integração e Resultado Final
A integral será calculada após a decomposição em frações parciais.
Integral Calculada!
Exemplos e Casos Especiais
Exemplo 1: Fatores lineares distintos
Função: (x+1)/(x²-1)
Decomposição: 1/(x-1)
Integral: ln|x-1| + C
Exemplo 2: Fatores repetidos
Função: 2/(x-1)²
Decomposição: 2/(x-1)²
Integral: -2/(x-1) + C
Exemplo 3: Denominador quadrático
Função: 1/(x²+4)
Decomposição: 1/(x²+4)
Integral: (1/2)arctan(x/2) + C
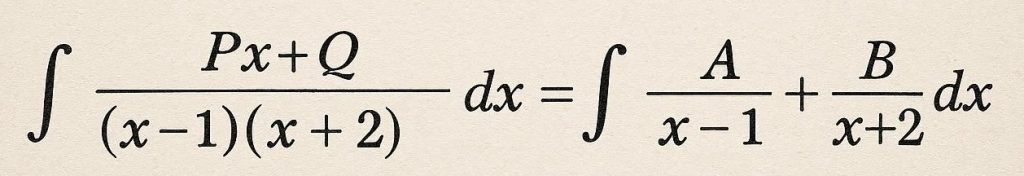
Método das Frações Parciais
Decompõe funções racionais em frações mais simples para facilitar a integração.
Casos de decomposição:
- Fatores lineares distintos: A/(x-a) + B/(x-b)
- Fatores lineares repetidos: A/(x-a) + B/(x-a)²
- Fatores quadráticos irredutíveis: (Ax+B)/(x²+px+q)
Fórmulas de integração:
∫ A/(x-a) dx = A·ln|x-a| + C
∫ B/(x-a)² dx = -B/(x-a) + C
∫ 1/(x²+a²) dx = (1/a)·arctan(x/a) + C
∫ x/(x²+a²) dx = ½·ln(x²+a²) + C