Calculadora de Comprimento de Arco
A calculadora de comprimento de arco é uma ferramenta para quem precisa determinar a extensão exata de uma curva em um intervalo definido.
Comprimento de arco
Calcule o comprimento de uma curva entre dois pontos usando cálculo integral.
Insira os parâmetros da função na calculadora de comprimento de arco
Como usar a calculadora de comprimento de arco
Primeiramente insira a Função f(x): A função cujo arco será medido
Em segundo lugar a Derivada f'(x): A derivada da função (opcional)
Em seguida o Limite inferior/superior: Intervalo para calcular o comprimento
Por fim, clique em Calcular para ver a solução passo a passo.
Sua configuração:
Fórmula e cálculo passo a passo
Fórmula do comprimento de arco:
A princípio, esta fórmula calcula o comprimento da curva y = f(x) entre x = a e x = b.
Insira os parâmetros acima e clique em Calcular.
Assim, você verá o cálculo completo passo a passo!
Comprimento Calculado!
Exemplos e visualização
Exemplo 1: Parábola
Função: f(x) = x²
Intervalo: [0, 2]
Derivada: f'(x) = 2x
Comprimento: ≈ 4.647 unidades
Exemplo 2: Seno
Função: f(x) = sin(x)
Intervalo: [0, pi]
Derivada: f'(x) = cos(x)
Comprimento: ≈ 3.820 unidades
Exemplo 3: Raiz Quadrada
Função: f(x) = x^(3/2)
Intervalo: [0, 4]
Derivada: f'(x) = (3/2)*x^(1/2)
Comprimento: ≈ 9.073 unidades
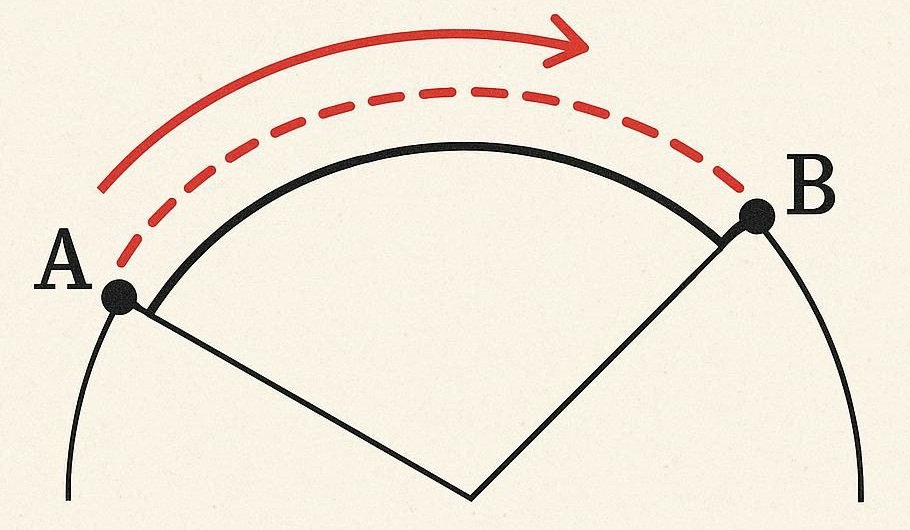
Interpretação Geométrica
O comprimento de arco é a distância ao longo de uma curva entre dois pontos.
Elementos da fórmula:
- f(x): Função que define a curva
- f'(x): Derivada (inclinação da curva)
- √(1 + [f'(x)]²): Comprimento do elemento infinitesimal
- ∫[a,b]: Soma de todos os elementos no intervalo
- L: Comprimento total do arco
Aplicações do comprimento de arco:
- Engenharia civil (cálculo de curvas em estradas)
- Arquitetura nos projeto de estruturas curvas
- Física na trajetórias de partículas
- Computação gráfica em renderização de curvas
- Robótica no planejamento de trajetórias suaves
- Teoria de cordas e membranas
- Cálculo de área de superfície de revolução
Além disso, a calculadora oferece um passo a passo detalhado, para estudantes, concurseiros que desejam compreender o processo por trás do resultado, e é muito utilizada em disciplinas como cálculo diferencial e integral, física e engenharia.