Calculadora de Coeficiente de Poisson: Online e Precisa

Quando você estica um elástico, ele não só fica mais longo também fica mais fino. Esse comportamento é descrito pelo coeficiente de Poisson. A princípio com nossa calculadora de coeficiente de Poisson, você descobre esse valor em segundos, usando apenas medidas simples de deformação.

Ou seja esse número é essencial em engenharia, materiais e até biomecânica. Seja para um projeto escolar ou uma análise técnica, entender como os materiais reagem em diferentes direções ajuda a evitar falhas e otimizar designs. Continue lendo e descubra como a física está em tudo que se deforma!

O que é o coeficiente de Poisson?

O coeficiente de Poisson (ν) mede a relação entre a contração lateral e o alongamento longitudinal de um material quando esticado. Por exemplo, ao puxar uma borracha, ela se alonga (deformação axial) e afinar (deformação transversal). Nesse sentido o coeficiente é a razão entre essas duas deformações, com sinal negativo para manter o valor positivo.

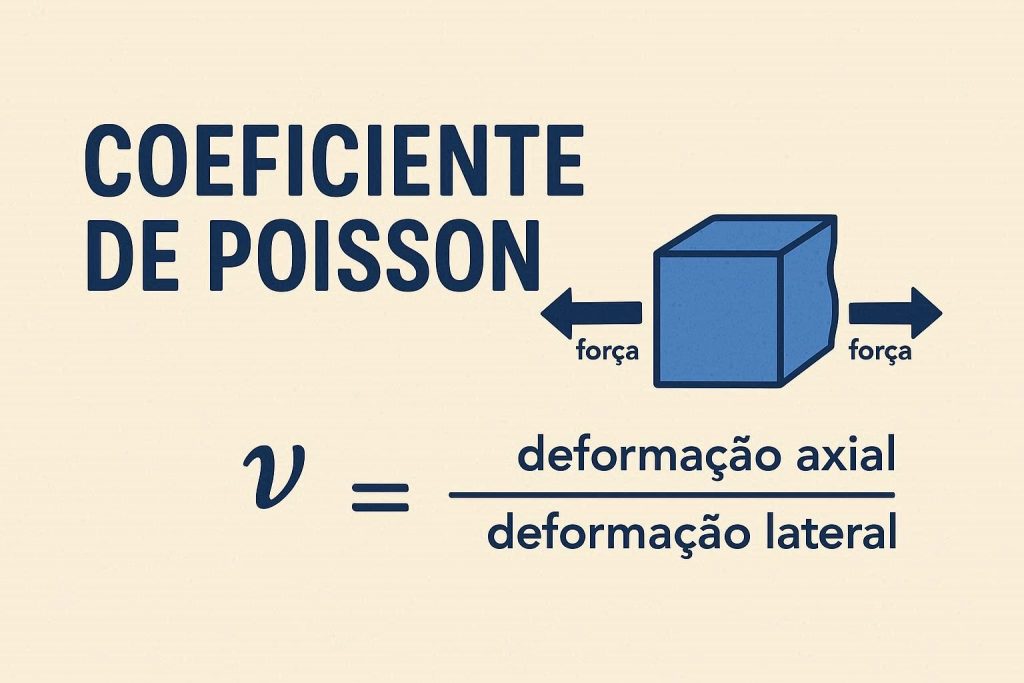
Enquanto a maioria dos materiais tem ν entre 0 e 0,5. A borracha está perto de 0,5 quase incompressível, enquanto o concreto fica em torno de 0,2. A calculadora transforma essas ideias em números reais, ajudando a comparar materiais com base em seu comportamento físico.

Como surgiu essa ideia?

O conceito foi introduzido pelo matemático francês Siméon Denis Poisson em 1829, ao estudar a elasticidade dos sólidos. Isto é ele percebeu que a deformação não ocorre apenas na direção da força aplicada, mas também perpendicularmente. Essa descoberta revolucionou a mecânica dos materiais.

Na atualizade, o coeficiente de Poisson é fundamental em simulações de engenharia, design de implantes médicos e até na indústria aeroespacial. Ferramentas digitais, como esta ferramenta, tornaram seu cálculo acessível a qualquer pessoa interessada em ciência dos materiais.

Quais as diferenças entre materiais compositos e metálicos?

Materiais isotrópicos como metais têm coeficiente de Poisson constante em todas as direções. Sendo assim os compósitos como fibra de carbono podem ter valores diferentes conforme a orientação das fibras são anisotrópicos. Porém, isso exige medições mais detalhadas e, às vezes, múltiplos coeficientes.

Como usar a calculadora de coeficiente de poisson passo a passo?

Primeiramente, tire as medidas de deformação axial alongamento dividido pelo comprimento original. Logo após, meça a deformação transversal encolhimento dividido pela largura original. Em seguida, insira os dois valores lembrando que a transversal geralmente é negativa. Clique em “Calcular” e obtenha o coeficiente de Poisson.

Por que é importante calcular esse coeficiente?

O coeficiente de Poisson afeta o desempenho de estruturas sob carga. Portanto ignorá-lo pode levar a deformações inesperadas, fissuras ou falhas em componentes críticos. Ele também é usado em modelagem de tecidos biológicos, pneumáticos e até calçados esportivos.

Quais as etapas do cálculo manual?

Em primeiro lugar: meça o alongamento (ΔL) e o comprimento inicial (L₀). Calcule εₐ = ΔL / L₀. Em seguida: meça a contração lateral (Δd) e o diâmetro inicial (d₀). Ai basta basta calcular εₜ = –Δd / d₀. Por fim: ν = –(εₜ / εₐ). Exemplo: εₐ = 0,008, εₜ = –0,0024 → ν = 0,30.

Embora simples, esse processo exige atenção aos sinais e unidades. Por isso, automatizar com a calculadora reduz erros e acelera o aprendizado especialmente em contextos educacionais.

Como fazer um experimento básico em casa?

Você pode usar um elástico grosso: meça seu comprimento e espessura com uma régua ou paquímetro. Estique levemente e meça novamente. Calcule as deformações e insira na calculadora. O resultado estará próximo de 0,5 típico de materiais elásticos.

Mesmo com recursos simples, é possível explorar conceitos avançados. E com a calculadora certa, transformar curiosidade em conhecimento é mais fácil do que parece.

Responsabilidade: Esta calculadora fornece estimativas com base em dados inseridos pelo usuário. Não substitui ensaios laboratoriais, laudos técnicos ou orientação de engenheiro ou cientista de materiais. Para aplicações críticas como estruturas, dispositivos médicos ou componentes industriais consulte sempre um profissional qualificado.